สมบัติของฟังก์ชัน
ฟังก์ชันคู่หรือคี่
ฟังก์ชันต่อเนื่องหรือไม่ต่อเนื่อง
ฟังก์ชันจำนวนจริง หรือ ฟังก์ชันเชิงซ้อน
ฟังก์ชันสเกลาร์ หรือ ฟังก์ชันเวกเตอร์
ฟังก์ชันคู่หรือคี่
ฟังก์ชันต่อเนื่องหรือไม่ต่อเนื่อง
ฟังก์ชันจำนวนจริง หรือ ฟังก์ชันเชิงซ้อน
ฟังก์ชันสเกลาร์ หรือ ฟังก์ชันเวกเตอร์
การประกอบฟังก์ชัน
ฟังก์ชัน f: X → Y และ g:Y → Z สามารถประกอบกันได้ ซึ่งจะได้ผลเป็นฟังก์ชันประกอบ g o f: X → Z ซึ่งมีนิยามคือ (g o f) (x) = g (f (x)) สำหรับทุกค่าของ x ใน X ตัวอย่างเช่น สมมติว่าความสูงของเครื่องบินที่เวลา t เป็นไปตามฟังก์ชัน h (t) และความเข้มข้นของออกซิเจนในอากาศที่ความสูง x เป็นไปตามฟังก์ชัน c (x) ดังนี้น (c o h) (t) จะบอกความเข้มข้นของออกซิเจนในอากาศรอบๆเครื่องบินที่เวลา t
ฟังก์ชันผกผัน
ถ้าฟังก์ชัน f: X → Y เป็นฟังก์ชันหนึ่งต่อหนึ่งต่อเนื่อง แล้ว พรีอิเมจของสมาชิก y ใดๆในโคโดเมน Y จะเป็นเซตโทน ฟังก์ชันจาก y ∈ Y ไปยังพรีอิเมจ f −1 (y) ของมัน คือฟังก์ชันที่เรียกว่า ฟังก์ชันผกผัน ของ fเขียนแทนด้วย f −1
ตัวอย่างหนึ่งของฟังก์ชันผกผันสำหรับ f (x) = 2x คือ f −1 (x) = x/2 ฟังก์ชันผกผันคือฟังก์ชันที่ย้อนการกระทำของฟังก์ชันต้นแบบของมัน ดู อิเมจผกผัน
บางครั้งฟังก์ชันผกผันก็หายากหรือไม่มี พิจารณา  ฟังก์ชัน
ฟังก์ชัน 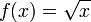 ไม่ใช่ฟังก์ชันผกผันเมื่อโดเมนของ
ไม่ใช่ฟังก์ชันผกผันเมื่อโดเมนของ  คือ
คือ 
 ฟังก์ชัน
ฟังก์ชัน 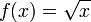 ไม่ใช่ฟังก์ชันผกผันเมื่อโดเมนของ
ไม่ใช่ฟังก์ชันผกผันเมื่อโดเมนของ  คือ
คือ 
ไม่มีความคิดเห็น:
แสดงความคิดเห็น