ฟังก์ชันหลายตัวแปร

 ฟังก์ชันหลายตัวแปร 

ฟังก์ชันที่เราใช้ส่วนมักจะเป็น ฟังก์ชันหลายตัวแปร ค่าที่ได้จะขึ้นอยู่กับปัจจัยต่างๆกัน จากมุมมองของคณิตศาสตร์ ตัวแปรทั้งหมดต้องแสดงอย่างชัดแจ้งเพื่อที่จะเกิดความสัมพันธ์แบบฟังก์ชัน - ไม่มีปัจจัย "ซ่อนเร้น" อยู่ และเช่นกัน จากมุมมองของคณิตศาสตร์ ไม่มีความแตกต่างเชิงคุณภาพระหว่างฟังก์ชันตัวแปรเดียวกับฟังก์ชันหลายตัวแปร ฟังก์ชันสามตัวแปรจำนวนจริงนั้นก็คือฟังก์ชันของ triple ((x,y,z)) ของจำนวนจริง

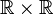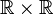ถ้าโดเมนของฟังก์ชันหนึ่งเป็นเซตย่อยของ ผลคูณคาร์ทีเซียน ของ n เซต แล้ว เราเรียกฟังก์ชันนี้ว่า ฟังก์ชัน n-ary ตัวอย่างเช่นฟังก์ชัน dist มีโดเมน  จึงเป็นฟังก์ชันทวิภาค ในกรณีนี้ dist ((x,y)) เขียนอย่างง่ายเป็น dist (x,y)

การดำเนินการ ก็เป็นฟังก์ชันหลายตัวแปรชนิดหนึ่ง ในพีชคณิตนามธรรม ตัวดำเนินการเช่น "*" นั้นนิยามจากฟังก์ชันทวิภาค เมื่อเราเขียนสูตรเช่น x*y ในสาขานี้ เสมือนกับว่าเราเรียกใช้ฟังก์ชัน * (x,y) โดยปริยาย เพียงแต่เขียนในรูปสัญกรณ์เติมกลาง (infix notation) ซึ่งสะดวกกว่า

ตัวอย่างที่สำคัญทางทฤษฎีตัวอย่างหนึ่งคือ กำหนดการเชิงฟังก์ชัน ซึ่งใช้แนวคิดของฟังก์ชันเป็นศูนย์กลาง ด้วยวิธีนี้ การจัดการฟังก์ชันหลายตัวแปรทำได้เหมือนเป็นการดำเนินการ ซึ่งแคลคูลัสแลมบ์ดา มีวากยสัมพันธ์ (syntax) ให้เรา